1998年全国大学生数学建模竞赛题目

A题 投资的收益和风险

市场上有n种资产（如股票、债券、…）Si ( i=1,…n) 供投资者选择，某公司有数额为M的一笔相当大的资金可用作一个时期的投资。公司财务分析人员对这n种资产进行了评估，估算出在这一时期内购买Si的平均收益率为，并预测出购买Si的风险损失率为。考虑到投资越分散，总的风险越小，公司确定，当用这笔资金购买若干种资产时，总体风险可用所投资的Si中最大的一个风险来度量。

购买Si要付交易费，费率为，并且当购买额不超过给定值时，交易费按购买计算（不买当然无须付费）。另外，假定同期银行存款利率是, 且既无交易费又无风险。（=5%）

    　

  1. 已知n = 4时的相关数据如下：

    　

    　

    Si

    (%)

    (%)

    (%)

    (元)

    S1

    28

    2.5

    1

    103

    S2

    21

    1.5

    2

    198

    S3

    23

    5.5

    4.5

    52

    S4

    25

    2.6

    6.5

    40

    试给该公司设计一种投资组合方案，即用给定的资金，有选择地购买若干种资产或存银行生息，使净收益尽可能大，而总体风险尽可能小。

    　

  2. 试就一般情况对以上问题进行讨论，并利用以下数据进行计算。

    　

　

Si

(%)

(%)

(%)

(元)

S1

9.6

42

2.1

181

S2

18.5

54

3.2

407

S3

49.4

60

6.0

428

S4

23.9

42

1.5

549

S5

8.1

1.2

7.6

270

S6

14

39

3.4

397

S7

40.7

68

5.6

178

S8

31.2

33.4

3.1

220

S9

33.6

53.3

2.7

475

S10

36.8

40

2.9

248

S11

11.8

31

5.1

195

S12

9

5.5

5.7

320

S13

35

46

2.7

267

S14

9.4

5.3

4.5

328

S15

15

23

7.6

131

　

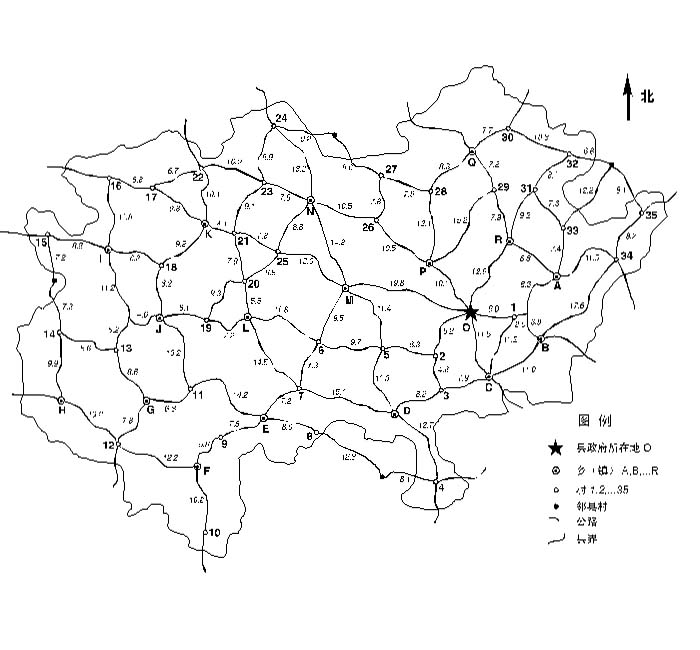
B题 灾情巡视路线

下图为某县的乡（镇）、村公路网示意图，公路边的数字为该路段的公里数。

今年夏天该县遭受水灾。为考察灾情、组织自救，县领导决定，带领有关部门负责人到全县各乡（镇）、村巡视。巡视路线指从县政府所在地出发，走遍各乡（镇）、村，又回到县政府所在地的路线。

    　

  1. 若分三组（路）巡视，试设计总路程最短且各组尽可能均衡的巡视路线。

    　

    　

  2. 假定巡视人员在各乡（镇）停留时间T=2小时，在各村停留时间t=1小时，汽车行驶速度V=35公里/小时。要在24小时内完成巡视，至少应分几组；给出这种分组下你认为最佳的巡视路线。

    　

    　

  3. 在上述关于T , t和V的假定下，如果巡视人员足够多，完成巡视的最短时间是多少；给出在这种最短时间完成巡视的要求下，你认为最佳的巡视路线。

    　

    　

  4. 若巡视组数已定(如三组），要求尽快完成巡视，讨论T，t和V改变对最佳巡视路线的影响。